是谁混淆了结果的真实性?
根据前几期的介绍,我们了解到临床研究的目的就是为了比较某暴露和非暴露情况对某人群或个体产生健康结局的差异即病因(causation)。最理想的情况下,就是使用一个个体或一个人群自身或完全相同的人群,而且在同一时间经历暴露和非暴露,然后比较健康结局。这个假象我们称为“反事实”(counterfactual),因为实际上这种比较是不可能的。现实就是,使用两个可比较的人群进行研究,尽量减少人群的差异对研究结果造成影响。
一旦脱离这种最理想的情况,我们获得更多的是关联(association)。那是什么混淆了结果的真实性呢?
从“相关”到“病因”,除了实验设计外,我们需要重点分析和排除的是:
1)随机误差;
2)系统误差(偏倚bias);
3)效应修正(effect modification)。
今天我们简单介绍这几个因素,并在未来的几期中将再分别详述。
1)随机误差:
- a.随机分布且不可预测的;
- b.不可避免但可估计误差大小;
- 通过增加样本量或重复测量取均值的方法可以减小。
2)系统误差即偏倚(bias):
- a.系统的偏离真实值;
- b.可避免,且必须控制。
偏倚:是指研究设计、实施、分析和推断过程中存在的各种对暴露因素与疾病关系的错误估计,它系统的歪曲了暴露因素与疾病间的真实联系。基本分为三大类:选择偏倚(selection bias)、信息偏倚(information bias)、混淆偏倚(confounding bias)。
3)效应修正(effect modification):
不像偏倚,效应修正是研究者需要去发现并报道的能够丰富暴露与结局关联关系的方式。
效应修正根据除暴露和结局变量外的第三类变量来改变暴露和结局之间的关联关系的大小。例如:
工作压力导致抑郁症;假设女性比男性更容易因为工作压力导致抑郁症,那么性别就是工作压力和抑郁症关联关系的一个修正因素(effect modifier)。我们应该分别报道在不同性别下工作压力与抑郁的关联关系,而不是去使用各种方法规避该因素。
在系统误差里面,我们特别关注的就是混淆偏倚(confounding)、选择偏倚(selection bias)和信息偏倚(information bias)。其中,信息偏倚(information bias)是指在研究的实施阶段中从研究对象获取研究所需的信息时产生的系统误差,其原因是由于诊断疾病、测量暴露或结局的方法有问题,导致被比较各组间收集的信息有差异而引入的误差。
混淆偏倚(confounding)
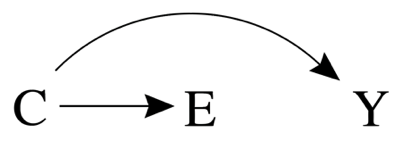
E:暴露变量(exposure);
Y:结果变量(outcome);
C:混淆因素
在研究暴露与疾病的联系时,C作为混淆因素(confounder)必须满足:
1)与exposure相关联;
2)与outcome相关联且不是因为exposure;
3)不在E和Y的因果链上。
但并不是满足这三个条件就是混淆因素。由于混杂变量的存在,造成了观察到的联系强度偏离了实际情况,则称为混杂偏倚。
小测试:
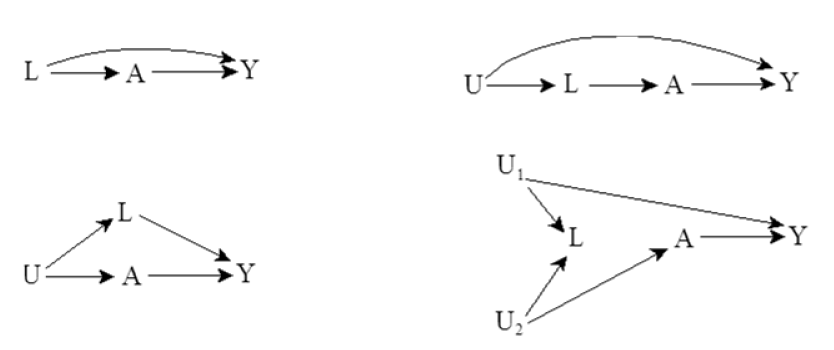
假设A=exposure,Y=outcome,哪些图的L不是混淆因素呢?
答案就是最后一个图。
混淆因素严重干扰我们对于risk的估计,所以必须想办法控制这些variable。但是有时候因为我们需要考虑的混淆因素不可测量,为了能够分析出真实的结果,可以使用surrogate confounder来控制混淆因素。
如下图:
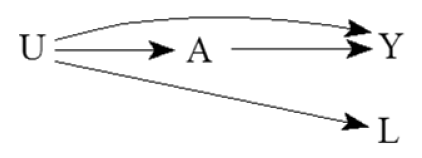
U为不可测量的混淆因素,为了控制U,我们可以替代使用能够代表U的其他变量L来分析。比如,我们需要考虑社会地位这个因素,因为无法测量社会地位,所以我们可以使用教育、收入、住址、学历等因素代表社会地位进行分析。
切忌:当进行统计分析的时候,务必仅考虑混淆因素而不对非混淆因素进行处理,所以并不是考虑的因素越多越好。因为分析时控制的混淆因素越多,则分析的power越低,甚至因为控制某一非混淆因素而引入新的混淆因素。如下图:
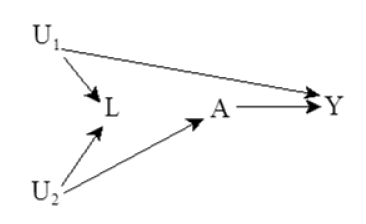
本身该DAG不存在混淆因素,但是如果误把L当成了混淆因素对其进行控制时,U1,U2则变成了混淆因素对A与Y的相关性产生干扰。
如何去除混淆因素对分析结果的影响呢?
在试验设计阶段,我们可以采取:
1)随机化(randomization):可以有效控制已知和未知的confounders;
2)匹配(matching)和限制(restriction):可以控制已知的confounders;
- 限制:如果认为某个或某些因素是可能的或已知的混杂因素,在设计过程中,可对研究对象的选择条件进行规定,但限制条件不宜太多。如研究冠心病与吸烟的关系,年龄与性别可能是混杂因素,就规定本次调查仅限于40-50岁的男性居民。
- 匹配(matching):个体配比将每个指示病例选择一个或多个对照,该对照与病例具有某些相同的特征,如年龄、性别等,在各比较组有相同的分布,以达到清除混杂作用的目的。频数配比将使对照组在某个潜在的混杂变量的分布与指示病例组的分布相同,如暴露组30-39岁为30%,40-49岁为30%,50-59岁为40%,那么非暴露组应与暴露组有相同的年龄分布。
3)选择不存在混淆因素与暴露相关的研究人群
在数据分析阶段,仅可以对已知的混淆因素进行控制。我们可以进行:
- IP weighting/standardization:通过标准化人群,让混淆因素在暴露和非暴露人群中的分布是相同的,从而去除混淆因素对分析结果的影响;
- stratification-based methods(包括stratified analysis, restriction, regression…):通过研究各个混淆因素水平下(假设各个水平下混淆因素不影响exposure和outcome的相关性),exposure和outcome的相关性以去除混淆因素对结果的影响。
选择偏倚(selection bias)
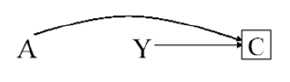
A:暴露变量(exposure)
Y:结果变量(outcome)
C:混淆因素(confounder)
选择偏倚(selection bias)是由于选择研究对象的方法有问题,使入选者与未入选者在某些特征上存在着系统差异,从而导致研究结果偏离真实情况。
选择偏倚是一个普适的概念,可以出现在随机对照试验、队列研究和病例对照试验。选择偏倚包括:失访(loss to follow-up)、无应答偏倚(non response bias)、数据缺失(missing data bias)、志愿者偏倚(volunteer bias)、self-selection、健康工人偏倚 (healthy worker effect)。在病例对照研究中,包括不合适选择对照组(inappropriate selection of controls)、入院率偏倚(Berkson’s bias)、现患病例偏倚(prevalence-incidence bias) 等。
入院率偏倚(Berkson’s bias)
在病例对照试验中需要考虑。指的是:利用医院或住院病人作为研究对象时,由于各种疾病的入院率不同而致的偏倚 。

A:吸烟
Y:膀胱癌
F:其他疾病
C:住院情况
在没有控制住院因素前,F=其他疾病并不是混淆因素;但是如果我们选择对照是仅在住院人群中筛选时,那么我们相当于人为的控制了C=住院情况。因为吸烟可能引起除膀胱癌以外的其他疾病,而这些疾病可能引起住院,因此,挑选的对照组具有相对于整体人群更高的吸烟率。因此,当我们分析吸烟与膀胱癌发生率的关系时受到混淆。
看一个例子再次说明:
| Hypothetical true association | Observed association | ||||
| Bladder cancer cases | Representative population controls | Bladder cancer cases | Hospital controls | ||
| 有吸烟史 | 75 | 40 | 75 | 70 | |
| 无吸烟史 | 25 | 60 | 25 | 30 | |
| OR | 4.50 | 1.29 | |||
可以很明显看到,住院人群中选择的对照组吸烟率明显较高,且会混淆真实的关联性分析。
现患病例-新病例偏倚 (prevalence-incidence bias)
在病例对照试验中需要考虑。指的是:在病例对照研究,调查时选择的病例往往是存活的现患病例,无法对那些因患病已死亡的病例或轻型、非典型或已痊愈的病例进行调查,而队列研究中常采用新发生的病例,因而病例对照研究得出的结论与队列研究的结果可能发生差异,此即现患病例-新病例偏倚,也称为奈曼偏倚(Neyman bias)。
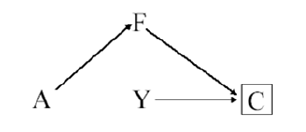
A:吸烟
Y:帕金森综合症
F:其他疾病(心脏病,肿瘤)
C:死亡情况
如上图,在没有控制死亡因素前,F=其他疾病并不是混淆因素;但是如果我们选择现患病人作为病例时,那么我们相当于人为的控制了C=死亡情况。因为吸烟可能引起除帕金森以外的其他疾病,而这些疾病可能引起死亡,这导致考虑本应该选入的病例因为提前死亡而被忽略,从而混淆了吸烟与帕金森发生的真实关系。
选择对照组不合适(inappropriate selection of controls)
在病例对照试验中需要考虑。
先看如下图:
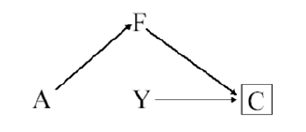
A:绝经后激素
Y:冠心病
F:髋骨折
C:选择进入试验
在选择对照病例前,F=髋骨折并不是混淆因素;但如果我们选择对照病例时考虑了髋骨折的情况,因为绝经后的激素影响髋骨折,如果排除或者入组髋骨折的病例,将可能影响对照组的绝经后激素的情况,从而混淆绝经后激素与冠心病发生的真实关系。
检出征候群偏倚(detection signal bias)
检出征候群偏倚是指某因素与某疾病在病因学上虽无关系,但由于该因素的存在会引起该病的临床症状或体征的出现,从而使患者及早就医,接受多种检查,导致该人群有较高的检出率,致使过高地估计该因素与该疾病的关联。
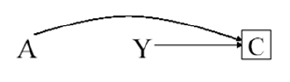
A:服用雌激素
Y:子宫内膜癌
C:子宫出血
举例说明:
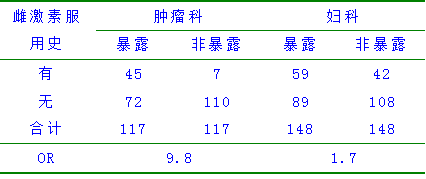
调查A=口服雌激素与Y=子宫内膜癌的关系。因为在人群中有一定量的无症状的子宫内膜癌早期病人,她们若不服用雌激素,子宫不致出血,因而不去医院就诊,而不能被发现,混淆了分析结果。如下表,肿瘤科医生发现子宫内膜癌患者雌激素暴露比例明显高于对照组,认为子宫内膜癌与服用雌激素密切相关。但是,妇科的发现却表明不相关,就是因为妇科同时考虑了子宫不出血的子宫内膜癌患者。
更年期服用雌激素与子宫内膜癌的关系
无应答偏倚 (non response bias) 和数据缺失(missing data bias)
无应答者是指研究对象中未按设计要求对被调查的内容予以应答者。某个特定样本中的无应答者的患病情况及某些因素的暴露情况与应答者可能不同,因此而产生的偏倚称为无应答偏倚。此种偏倚在分析性研究和实验性研究中均可发生。
失访偏倚(loss to follow-up)
失访也是无应答的一种表现,只是它主要发生在队列及实验性研究中。在随访研究过程中,研究对象未能按计划被随访,它是此类研究选择偏倚的主要原因之一。
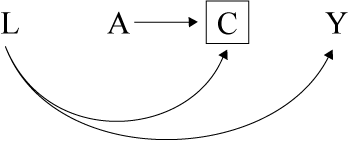
A:外来人口(migrant)
Y:肿瘤
L:收入
C:失访
失访偏倚就是在比较组间病例的随访完整度不同。如上图,想要研究A=外来人口与Y=肿瘤发生的关系。但是外来人口当生病时,根据L=收入水平的不同选择回到老家进行治疗或留在工作地治疗。因此,外来人口较容易导致失访,并且因收入水平低造成的失访导致随访的外来人口无法代表整体外来人口的情况,最终造成结果偏倚。
志愿者偏倚(volunteer bias)和self-selection
一般情况下,志愿者与非志愿者在关心健康、注意饮食习惯、禁烟、禁酒及体育锻炼等方面可能存在系统的差别,因而,志愿者被入选为观察对象,而非志愿者落选,这样的研究结果往往有选择偏倚。
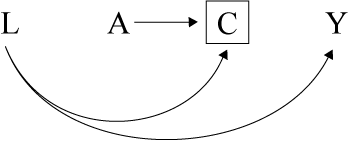
A:吸烟
Y:冠心病
L:心脏病关注意识(家族心脏病史)
C:志愿或被选择参与研究
当研究A=吸烟和Y=冠心病的关联性时,对于有家族心脏病史的人群往往会感觉到容易得冠心病而更愿意参与研究,且有家族心脏病史的志愿者确实更容易患心脏病,因此容易造成结果的偏倚。
健康工人偏倚 (healthy worker effect)
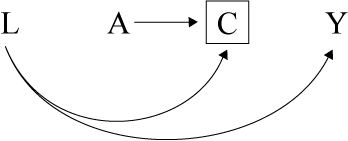
A:职业暴露
Y:死亡
L:体检
C:在职
当研究A=职业暴露和Y=死亡的关联性时,因为体检的关系,身体状况不佳的员工比较容易离职,而留下继续工作的往往是身体状况较好的。当仅以C=在职的员工作为受试者的情况下,容易低估职业暴露对死亡的影响。
如何控制选择偏倚对分析结果的影响呢?
1.正确的研究设计
首先研究者对整个研究可能会产生的各种选择偏倚有充分的了解。在设计中,应注意使被比较的各组有同等的概率受到调查。应考虑可能出现的各种偏倚,以及会在那些环节出现,只有在设计时考虑周全,并采取相应措施,在各个环节中阻断偏倚产生的可能性,才能防止或减少其发生。
2.尽量采用多种对照
理想的是以人群中全体病例和非病例(或其有代表性的样本)作为研究对象。如以医院病例为研究对象,宜在多个医院选择对象,且最好有2个对照组,其中一个对照组来自社区一般人群,在队列研究中,最好也应设多种对照,以减少选择偏倚对结果的影响。
3.严格掌握研究对象入选与排除的标准
使研究对象能较好地代表其相应的总体。如病例对照,一般可规定病例的入选原则为新发的确诊病例,以避免Neyman偏倚。在实验性研究中,应严格按照随机分配的原则,将研究对象分组,使两组除所观察因素外应具有均衡性、可比性。应避免将志愿者分为一组,非志愿者分为另一组,病情轻者分在一组,病情重者分在另一组等情况的发生。
4.提高研究对象的依从性
在研究中应采取相应措施,尽量取得研究对象的合作,尽可能提高应答率,减少无应答率和队列研究中的主动失访,要做好组织、宣传工作,调查手段要简便易行,对调查中的问题应采取适当的处理技巧。若无应答或失访者超过10%,应对无应答者或失访者进行随机抽样调查,对失访者和已随访者的特征做比较分析。对研究结果可能有影响有关数据与应答者进行分析比较,若两者差异有显著性,说明对结果有影响,在结论中应加以说明并应作慎重的分析。
5.当试验设计无法避免选择偏倚时,使用统计方法进行去除:
1)分层分析
2)IP weighting
方法同混淆因素分析。
